BÉZIER-KURVEN UND DEREN ANWENDUNGEN IN DER COMPUTERGRAFIK UND DER GEOMETRISCHEN MODELLIERUNG – Walter Schupeck
Schlüsselwörter: Bézier-Kurven, Computergraphik, CAGD, CAD
Einleitung
Im Rahmen dieser Präsentation im Umfang von wenigen Seiten kann das Thema „Bézier-Kurven und deren Anwendungen in der Computergrafik und der geometrischen Modellierung“ nicht in voller Breite dargestellt werden, da es ein großes thematisches Spektrum abdeckt und die Bézier-Kurven in der Computergraphik [1] auf sehr vielen Gebieten zur Anwendung kommen.
Ich werde deshalb die mathematische Theorie der Bézier-Kurven in einem ersten Kapitel nur sehr verkürzt darstellen. Trotz aller Beschränkung möchte ich jedoch kurz auf die beiden Forscher Casteljau und Bézier eingehen. Beide suchten nach konkreten Lösungen für Aufgabenstellungen aus der technischen Konstruktion, welche sich aus ihrer Arbeit als Ingenieure in der Automobilindustrie ergaben und damit verweisen deren berufliche Wirkungsfelder auf eines der wichtigsten Anwendungsgebiete: CAD/CAM, zu dessen Erfolg beide Forscher elementare Beiträge geleistet haben.
Nach einem ebenfalls kurzen und deshalb längst nicht vollständigen Überblick über die wichtigen Anwendungsgebiete in der Computergraphik – mit einer mehr stichwortartigen Beschreibung – werden exemplarisch und schwerpunktmäßig ausgewählte Anwendungsgebiete und der Kontext der Anwendung von Bézier-Kurven etwas ausführlicher dargestellt und erläutert.
Mathematische Grundlagen
Die Bézier-Kurven wurden in den 60igern von Bézier und Casteljau unabhängig voneinander gefunden und sind seither ein zentrales mathematisches Methodenwerkzeug zur Darstellung von Kurven und Flächen in der Computergraphik.
Innerhalb der an sich schon hoch innovativen, dynamischen Informationstechnologie stellt die Computergraphik mit ihren spektakulären Merkmalen eine extrem dynamische Disziplin dar, die eine Vielzahl von Anwendungsgebieten durchdrungen hat und dabei die Bézier-Kurven zur Anwendung gebracht hat. Wir finden deshalb Anwendungen von Bézier-Kurven in vielen wissenschaftlichen Disziplinen und bei der Benutzung von PCs im täglichen Leben.
Bevor nun auf die Anwendungsgebiete im Einzelnen eingegangen wird, sei an dieser Stelle in aller Kürze die von jedem Mathematiker als bestechend schön empfundene Theorie der Bézier-Kurven dargestellt.
Bézier-Kurven und der Algorithmus von Casteljau
Die Grundbausteine für Bézier-Kurven sind die Bernsteinpolynome. Die aus den binomischen Formeln ableitbaren Bernsteinpolynome über dem Intervall [a,b] vom Grad n stellen sich wie folgt dar:
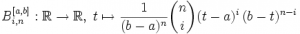 |
(1) |
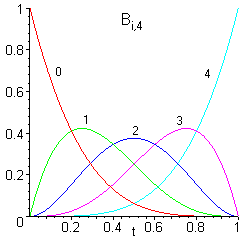
Die Bernsteinpolynome sind linear unabhängig und bilden eine Basis des Polynomraumes Ρn. Die Bernsteinpolynome Bi,4 vom Grad 4 sind in der Abbildung 1 dargestellt.
| Abbildung 1 Bernsteinpolynome Bi,4 , 0 ≤ i ≤ n vom Grad 4 |
 |
| Quelle: http://upload.wikimedia.org/wikipedia/de/8/81/Bernsteinpolynom.png |
Die wichtigsten Eigenschaften der Bernsteinpolynome bezüglich des Intervalls [0,1] lassen sich in Abb. 1 gut erkennen [2]:
| Bi,n(t) = Bn − i,n(1 − t) | (2) | Symmetrie (Spiegelachse bei t=0,5 | |
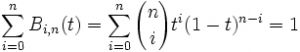 |
(3) | Partition der 1 (Summe einem Zeitpunkt t ist 1 | |
| |
(4) | Rekursion | |
| Bi,n(t) > 0 für alle t € (0,1) | (5) | Positivität |
Eine Bézier-Kurve n-ter Ordnung mit den so genannten Kontrollpunkten Pi stellt sich nun auf dem Interfall 0 ≤ i ≤ 1 dar wie folgt:
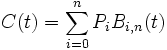 |
(6 ) Bézier-Kurve | |||
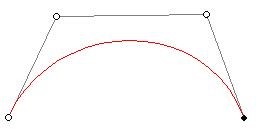
| Abbildung 2 Bézier-Kurve Grad 3 | ||||
 |
||||
Sie besteht also aus n Kontrollpunkten, die mit den Bernsteinpolynomen gewichtet sind. Da, wie man in Abb. 2 gut erkennt, die Bézier-Kurve innerhalb der konvexen Hülle des Kontrollpolygons liegt und sich an dieses annähert, eignen sich Bézier-Kurven hervorragend für generatives, durch ein graphisches User-Interface unterstütztes Entwerfen am Bildschirm. Neben der Invarianz gegenüber affinen Transformationen seien hier noch zwei weitere Eigenschaften ohne vertiefende Darstellung kurz benannt:
- Kurve geht durch Anfangs- und Endpunkt des Kontrollpolygons
- Kurve ist an den Endpunkten tangential zu P1-P0, Pn– Pn-1 .
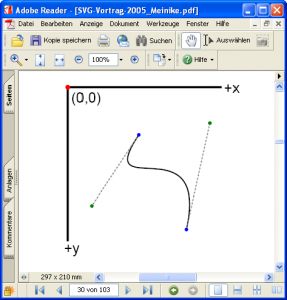
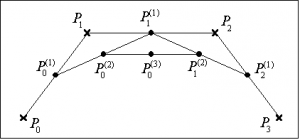
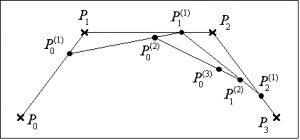
Von zentraler Bedeutung zur Generierung und schnellen Berechnung einer Bézier-Kurve mittels eines Polygonzuges ist der Algorithmus von de Casteljau, der in Abb. 3 in seiner geometrischen Interpretation dargestellt ist. Durch fortgesetztes Zerteilen von Linien kann der gewünschte Kurvenpunkt approximiert werden, dabei werden die Verbindungsstrecken im Verhältnis t geteilt. Dies wird solange fortgesetzt, bis die Rekursion abbricht. [3]
| Abbildung 3 Algorithmus von de Casteljau; n=3, t=1/2 und t= 3/4 | |
  |
|
| Quelle: http://www.apm.tuwien.ac.at/docs/lva/mmgdv/k1/k1___097.gif | |
Um noch komplexere Kurven generieren zu können werden Splines verwendet. Dabei handelt es sich um mehrere Kurven, welche an ihren Randpunkten mit bestimmten Anforderungen zusammengesetzt werden. Werden dabei Bézier-Kurven für die Segmente verwendet, spricht man von Bézier-Splines. In der Regel werden kubische Bézier-Kurvenabschnitte verwendet und es können komplexe Kurven der Computergraphik erzeugt werden, wie z.B. Outlines von Buchstaben und Logos. An den Knotenpunkten werden je nach Anwendung unterschiedliche Stetigkeitsanforderungen C1 bzw. C2 gefordert.
B-Splines bestehen nun aus Kurvensegmenten, welche verallgemeinerte Bernstein-Polynome darstellen. Sie sind damit den Bézier-Splines verwandt, haben erhebliche Bedeutung im Bereich Computer Aided Geometric Design, führen hier aber über das Thema hinaus.
Die Anforderung Freiformkurven zu definieren und Werkstücken festgelegte Kurvenformen aufzuprägen gab es bereits in der Zeit der Griechen und Römer bei der handwerklichen Fertigung. So wurden bei der Herstellung von Schiffrümpfen Musterhalterungen verwendet, um Schiffsrippen die benötigte Form „aufzuzwingen“. Die Musterhalterungen bestanden aus 2 Bolzen, in welche die zu formenden Holzrippen eingespannt wurden. Es waren damit die Endpunkte als auch die Tangenten vorgegeben und aus physikalischen Gründen musste sich eine kubische Bézier-Kurve einstellen. Mit Hilfe der Musterhalterungen musste die Freiformkurve nur einmal entworfen und anschließend reproduziert werden. Diese Technik wurde im späten Mittelalter von venezianischen Schiffsbaumeistern weiter verfeinert.
Was in der Computergraphik als mathematischer Fachterm „Spline“ eingeführt ist, wurde bereits im 17ten Jahrhundert als Begriff verwendet. In der Schiffbautechnik wurden „Splines“, dünne Holz- oder Metalllatten (Straklatten), mit Gewichten fixiert. Es stellte sich damit eine Form ein, welche die 2.Ableitung minimiert. Es ergab sich damit eine glatte Kurve für den Schiffrumpf mit optimierter Verteilung der Belastung bei größter Festigkeit.
Anfang des 20igsten Jahrhunderts wurde verstärkt nach mathematischen Lösungen gesucht, jedoch ohne Erfolg. Erst Paul de Faget de Casteljau entdeckt 1959 die Bernsteinpolynome, als Grundbaustein der Bézier-Kurve
Pierre Bézier, der weltberühmte Industrieforscher auf dem Gebiet CAD/CAM und schlechthin der Pionier auf dem Forschungsgebiet der interaktiven Generierung von Freiformkurven und -flächen, war der erste der in den 60iger Jahren die später nach ihm benannten Bézier-Kurven beschrieb und seine Forschungsergebnisse auch veröffentlichen konnte. Er wurde am 1. September 1910 in Paris geboren. Sein erstes Studium in Maschinenbau schließt er 1930 und sein zweites Studium 1932 in Elektrotechnik ab. Er beginnt seine berufliche Karriere 1933 bei Renault, wo er 42 Jahre arbeitete und forschte und verschiedene Führungsfunktionen unter anderem als Leiter der Produktionsplanung, innehatte.
Seit den frühen 60iger Jahren konzentrierte er sich auf die Forschungsgebiete, die ihn weltbekannt machten. Ein wesentlicher Teil seiner Zeit ging dabei in die Entwicklung des CAD/CAM-Systems UNISURF von Renault ein, welches seit 1968 bei Renault produktiv angewendet wird und gegenwärtig von ca. 1500 Anwendern genutzt wird.
Im Jahr 1968 wird Pierre Bézier Professor an „Conservatoire Nationale des Arts et Métiers“, wo er dann bis 1979 lehrte und forschte. Er stirbt am 25. November 1999 als Ehrenmitglied der American Society of Mechanical Engineers.
Paul de Casteljau entdeckte 1959, also früher und unabhängig von Bézier, die Bézier-Kurve und das zugrunde liegende Konstruktionsprinzip, da jedoch Citroën die Forschungsergebnisse bis Ende der 60iger Jahre geheim hielt, war es Bézier, der als erster darüber publizierte. Erst nach einem Vergleich in einem Rechtstreit wurde die Leistung von Casteljau anerkannt. Seither wird die allgemeine Formel und damit die Kurven nach Bézier benannt (Bernstein-Bézier-Polynom, Bézier-Kurve) und das Konstruktionsprinzip wird nach De Casteljau (De Casteljau-Algorithmus) benannt.“
Bézier und Casteljau waren große Pioniere des Forschungsgebietes Computer Aided Geometric Design und ihre Algorithmen sind heute in jedem CAD- und Zeichenprogramm von AutoCAD bis CATIA von Dassault implementiert. Beide sind auch Symbole für die Leistungsfähigkeit der anwendungsorientierten, industriellen Forschung und Entwicklung der europäischen Automobilindustrie. Ein Nachruf von Paul Cox hält fest: „The Bezier Curve changed world“. [6]
Da die Anforderung Freiformflächen und Freiformkurven zu konstruieren und darzustellen in vielen wissenschaftlichen und technischen Disziplinen auftritt, hat sich die Anwendung von Bézier-Kurven nach ihrer Entdeckung sehr rasch verbreitet. Heute kommen sie auf sehr vielen Gebieten zum Einsatz. Massiv beschleunigt wurde dieser Prozess durch die permanente Leistungssteigerung von Rechnerhardware und Graphikhardware bei fallenden Preisen. Da die Funktionalitäten Freiformflächen und Freiformkurven in viele Systeme und Produkte der Informationsindustrie im allgemeinen und der Computergraphik im besonderen eingeflossen und implementiert worden sind, ist die Anwendung oder Nutzung dieser Funktionen etwas Alltägliches in Forschung und Technik geworden.
Ohne Vollständigkeit anzustreben sei an dieser Stelle ein Überblick über wichtige Anwendungsgebiete in der Computergraphik gegeben und die dabei zu Einsatz kommenden Computergraphiksysteme oder -technologien kurz beschrieben.
- Modelling im Computer Aided Geometric Design: Eines der wichtigsten Anwendungsgebiete ist die gesamte Prozesskette CAD/CAM mit ihren unzähligen Produkten und Applikationen. Durchweg alle marktfähigen CAD-Systeme und hochwertigen IT-Systemkomponenten der Fertigungsautomatisierung von Werkzeugmaschinen, über Robotersysteme und flexible Fertigungssysteme haben Funktionen zur Generierung und Verarbeitung von Bezierkurven implementiert. Wegen seiner Bedeutung und wegen des persönlichen Bezugs des Autors wird dies in einem eigenen Kapitel weiter vertieft.
- 3-D Visualisierung und Computer Animation: In diesen Anwendungsgebieten wird die polygonale Modellierung (Punkte, Kante, Fläche) mehr und mehr durch Bézier-Kurven ersetzt. Organische Körper und andere Objekte mit gekrümmten Oberflächen werden mit Bézier-Kurven und verwandten Methoden (Bézier-Patch-Modelling) erstellt, wobei tangentiale Patch-Übergänge mit Bézier-Kurven definiert werden. In Animationenprogrammen kommen Bézier-Kurven zum Einsatz, sowohl zur Definition von Pfaden an denen sich Objekte entlang bewegen sollen, als auch als so genannte IPO Kurven um die Eigenschaften von Objekten mit der Zeit zu ändern [7]. Es lässt sich heute festhalten: Ohne Splines und Bézier-Kurven gäbe es kein Jurassic Park und keine Lara Croft [8].
- holographischer Oberflächen: Auf dem Gebiet der Multimediatechnik wird an Systemen mit holographischen Oberflächen gearbeitet, wo das Mensch-Maschine-Interface die manuelle Manipulation von Objekten ermöglicht [9], und eine Verschiebung in Relation zu zwei Kontrollpunkten einer Bezierkurve ausgelöst werden kann, so der Prototyp Holowall von der Firma Sony [10].
- Illustration und Zeichnung: Illustrations-Programme oder Zeichen-Programme zur interaktiven Erzeugung von Zeichnungen oder Illustrationen (Adobe Illustrator), also Vektorgraphik-Programme, verfügen in der Regel über Bézier-Werkzeuge. Adobe Illustrator kam 1984 auf den Markt und war eines der ersten Programme, welches mit Bézier-Kurven umgehen konnte. Auch Bildbearbeitungsprogramme, mit denen Bitmap-Graphiken erzeugt (Adobe Photoshop), optimiert und geändert werde können, verfügen über Bézierfunktionalitäten.
- Mikro- und Detailtypografie: Hier werden Bézier-Kurven zur Konstruktion der Kontur von Schriftenzeichen und Zeichen verwendet.
- Programmierung: Bei der Programmierung werden natürlich Bézier-Kurven implementiert, die eben in den hier dargestellten Applikationen der Computergraphik benötigt werden. Oft stehen APIs zur Verfügung wie zum Beispiel Microsoft Windows Graphics Device Interface (GDI) im 2D-Bereich.
- Bézierprimitive in Vektorgraphikformate: So enthält das Scalable Vector Graphics Format (SVG), ein XML Standard zur Beschreibung zweidimensionaler Vektorgrafiken, so genannte Bézierprimitive.
- Geo Informationssysteme und viele andere Anwendungen: Es gibt viele weitere Anwendungen von Bézierkuven: GIS Systeme und andere Systeme der Kartographie, Archäologie und Architektur. In seiner Dissertation „Bernstein-Bézier Representations for Facial Surgery Simulation” untersuchte Roth die Anwendung auf dem Gebiet der Simulation von kieferchirurgischen Eingriffen. [[1]1]
In den nächsten Kapiteln werden nun ausgewählte Anwendungsgebiete exemplarisch umfassender erläutert: Modelling im Computer Aided Geometric Design, Vektorgraphikenformate, Bézierwerkzeuge in Konsumer-Software zur Illustration und Mikro- und Detailtypografie.
Konstrukteure kommen im Maschinenbau ohne Freiformkurven und –flächen nicht aus, weil sie sonst auf analytische Kurven wie Kreis, Ellipse, Parabel, Hyperbel und analytische Flächen wie Kugel usw. beschränkt wären. Insbesondere für den Karosseriebau, Flugzeugbau, Schiffsbau, Turbinenbau, Gießereiwerkstücke besteht ein erheblicher Bedarf an Methoden zur Generierung und Darstellung von Freiformkurven und –flächen. So wurden in der Automobilindustrie vor der Entwicklung der Bézier-Kurven die Kurven aus Zeichenpapier mittels Kurvenlineal gezeichnet, vergleichbar auf Bild 2 im Bildanhang. Die Skizze musste mit viel Aufwand auf ein maßstäbliches Modell aus Holz und Ton übertragen werden. Ein letztes Mastermodell wurde aus Gips hergestellt, welches dann zur Formgebung für die Karosseriepresswerke diente. Es war deshalb für die Forschungs- und Entwicklungsbereiche der Automobilhersteller ein sehr wichtiges Ziel im Designprozess frei geformte Kurven und Oberflächen darstellen zu können und damit effektiver zu werden.
Anfang der 60iger Jahre waren durch ausreichend leistungsstarke Hardware und Systemsoftware der IBM-Großrechnersysteme die Voraussetzungen gegeben um einsatzfähige CAD-Systeme zu schaffen. Führend waren dabei die Flugzeughersteller wie Lockheed in den USA, Dassault in Frankreich und die großen Automobilhersteller wie Renault, Citroen und Mercedes, die an Systemen für ihren eigenen Bedarf arbeiteten und ihre Ergebnisse meist nicht veröffentlichten, sondern oft streng als Betriebsgeheimnis schützten. Nachdem Bézier seine Entdeckung der Bézier-Kurve publizierte, wurden seine Forschungsergebnisse von der damals noch sehr kleinen CAGD-Community sofort aufgegriffen und die vorhandenen Systeme um Freihandkurven mittels Bézier-Kurven erweitert. Neben dem bereits erwähnten Programm CAD/CAM-Systems UNISURF sei hier noch das Programm CATIA von Dassault genannt, mit welchem die Mirage als erstes Flugzeug entwickelt wurde und welches heute Markführer ist. Gegenwärtig wird CATIA bei Boeing, Airbus, DaimlerChrysler, BMW, Peugeot, Citroën, Ford und auch bei Toyota eingesetzt.
Mit dem Aufschwung der Unix-Workstations und PCs in den 80iger entwickelte sich dann ein Massengeschäft mit marktreifen Produkten. Mit AutoCAD wurde 1982 ein erstes PC-CAD präsentiert, welches bereits über Bézier-Kurven verfügt. Es entstand ein großer Markt für CAD-Systeme.
Der Autor selbst war z.B. 1988 als Softwareentwickler an der Produktentwicklung des Unix-basierten Systems Nestler CAD beteiligt, wo er unter anderem Funktionalitäten wie Bézier-Kurven und Splines programmierte und in das Gesamtpaket implementierte. Dieses System ist heute noch unter dem Namen NesCAD 2004 im Einsatz und erhält weiterhin Support. Etwas später war er an der Entwicklung eines CAD-Prototyps zum Design von Uhren für den schweizerischen Uhrenhersteller Swatch beteiligt, wo Funktionalitäten wie Bézier-Kurven und Splines zum Pflichtenheft gehörten.
Heute gibt es weltweit über 1000 CAD-Systeme mit Funktionen auf Basis von Bézier-Kurven. Einer der Marktführer wie z.B. AutoCAD hat eine Installationsbasis von mehr als 2 Millionen.
- Bézierwerkzeuge als Standardmodul von Konsumer-Software
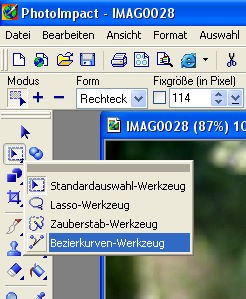
Es gibt eine Unzahl von Programmen, die in großen Stückzahlen zu kleinen Preisen als Massenprodukte verkauft werden und als Software von jedermann genutzt werden und welche als Basisfunktionalität ein so genanntes Bezierkurven-Werkzeug haben. Dazu gehört Software zur Bildbearbeitung, wie z.B. PhotoImpact, Jasc Paint Shop Pro, Photoline und Microbasic Photo Master Suite.
| Abbildung 4 Bezierkurven-Werkzeug bei PhotoImpact |
 |
| Quelle: PhotoImpact 10 |
Ein Bildschirmabzug am Beispiel von PhotoImpact zeigt die Abbildung 4. Eine weitere Gruppe sind vektorbasierte Grafik- und Zeichenprogramm, wie z.B.Adobe Illustrator, CorelDRAW, Corel Designer und Macromedia Freehand um hier die populärsten zu nennen. Adobe Illustrator, eines der ersten vektorbasierten Graphikprogramme, konnte bereits1985 mit Bézier-Kurven umgehen.
- Bézier-Kurven im WWW-Standard Scalable Vector Graphics [13]
Scalable Vector Graphics (SVG) baut auf XML auf und dient der Beschreibung von Vektorgraphiken, welche mit einem Plug-In im Browser dargestellt werden. SVG wurde 2001 vom World Wide Web Consortium mit dem Ziel verabschiedet einen neuen Standard zu schaffen. Bézier-Kurven gehören zu den graphischen Formen von SVG.
Sie haben als so genannte Pfade die folgende Notation:
<path d=“…“/>, D = Pfad-Daten mit Parametern wie folgt [C,c] x1, y1 x2,y2 x,y ::Cubic Bézier curveto
[S,s] x2,y2 x,y ::Smooth cubic curveto
[Q,q] x1, y1 x,y ::Quadratic Bézier curveto
Die verlustfreie Skalierbarkeit macht Vektorgraphik für den Printbereich unersetzbar, weil damit die höchstmögliche Auflösung des jeweiligen Ausgabegerätes genutzt werden kann. Zu den bekannten Vektorgraphik-Softwarepaketen gehören z.B. Adobe Ilustrator, CorelDraw, Adobe FreeHand, Xara Xtreme, Canvas, Lineform und Microsoft Expression Design.
Die Bezierkurven haben sehr schnell nach ihrer Entdeckung ein Anwendungsfeld durchdrungen, mit dessen Produkten gegenwärtig zwangsläufig alle tun haben, die einen PC nutzen, da die menschliche Kommunikation eben auf Schriften basiert. Dies sind Computerschriften in Form von Schriftfonts. Die ersten Zeichensätze, die zu Beginn der elektronischen Datenverarbeitung zum Einsatz kamen, waren Bitmap-Fonts. Jeder Buchstabe wird durch ein Matrix-Raster repräsentiert. Diese Lösung ist zwar sehr einfach, hat aber den Nachteil, dass die Zeichen nicht skalierbar sind. Wegen dieser konstruktiven Schwäche sind Bitmap-Fonts auf modernen Systemen fast vollständig von PostScript und TrueType verdrängt worden.
PostScript ist eine interpretierte auf Forth basierende Programmiersprache, um auf einfache Art und Weise Buchstaben, Text und vergleichbare zweidimensionale Grafiken hardwareunabhängig zu beschreiben. Zu Optimierung der Druckausgabe wird der Interpreter direkt in den Druckercontroller platziert um die Rastergraphik zu erzeugen. PostScript Type1 war eines der ersten Outline-Fontformate welches von Adobe für PostScript Mitte der 80er Jahre entwickelt wurde. Die Kurvenbeschreibung der PostScript-Type1-Fonts basiert auf kubischen Bézier-Kurven. PostScript Type1 war der Fontstandard im Grafikdesign und der Druckvorstufe [14]. Es wird jedoch wegen schlechter Bildschirmoptimierung und fehlender Unicode-Unterstützung immer mehr durch TrueType und OpenType, einer Weiterentwicklung des TruType-Formates, abgelöst.
- TrueType-Schriften und OpenType [15]
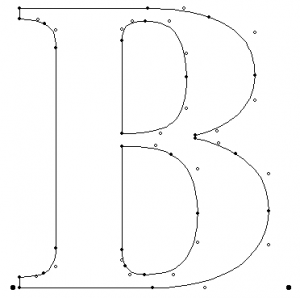
Das TrueType-Format war Ergebnis einer strategischen Allianz von Apple und Microsoft um die Abhängigkeit von Adobe zu reduzieren, aber auch um technische Verbesserungen einzuführen. TrueType basiert auf Sequenzen von quadratische Bezier-Kurven wie in Abbildung 6 gezeigt.
| Abbildung 6 TrueType Zeichen |
 |
| Quelle: http://www.mediaforum.ch/fachlexikon/fachbeitraege/true_type.html |
Erst durch den Rasterizer werden die nötigen Bildpunkte für die Bildschirmdarstellung bzw. Seitenlayoutdarstellung vor der Ausgabe berechnet. Das Open-Type Format stellt nur eine Weiterentwicklung von TrueType dar und ermöglicht die „Ko-Existenz“ von PostScript und TrueType Fonts.
Abbildung 6 zeigt Glyphe B, als Serie von Punkten, so genannte „on-curve“ oder „off-curve“ Punkte. Mit 3 Punkten, zwei on-curve-Punkten an den Enden und einem dritten off-curve-Punkt außerhalb der Geraden wird eine quadratische Bézier-Kurve festgelegt.
- Schlussfolgerung und Ausblick
Die von Bézier und Casteljau entdeckten Bézier-Kurven und die darauf basierenden Methoden und Modelle sind heute ein unverzichtbares und wesentliches Werkzeug zur Darstellung und Verwendung von Kurven und Flächen in der Computergraphik. Diese beiden herausragenden Wissenschaftler stehen für die Innovations- und Leistungsfähigkeit der angewandten Forschung bei den führenden europäischen Automobilherstellern.
Vom Modelling im Computer Aided Design über Computer Animation bis zum Einsatz auf dem Gebiet der Simulation von chirurgischen Eingriffen haben die Anwendungen von Bézier-Kurven alle Bereiche von Wissenschaft, Forschung, Industrie bis zur Kunst durchdrungen. Mit der Dynamik der Computergraphik und ihrer vielen Teildisziplinen wird es auch in Zukunft weitere viel versprechende neue Anwendungsmöglichkeiten von Bézier-Kurven geben.
Glossar
| CAD | „Der Begriff Rechnerunterstützte Konstruktion oder englisch Computer Aided Design (CAD) bezeichnet eine Art „elektronisches Zeichenbrett“.Mit CAD-Programmen erstellt man nicht nur technische Zeichnungen. Mit den aufwändigeren Programmen werden zunächst einmal dreidimensionale Volumenmodelle erstellt. Daraus können zwei- oder dreidimensionale Zeichnungen und sogar bewegte Visualisierungen der Objekte abgeleitet werden. CAD-Software kommt in allen Fachbereichen, in denen Konstruktionen entwickelt werden, zur Anwendung: zum Beispiel im Anlagenbau, Maschinenbau, Schiffbau und auch in der Architektur und im Bauwesen.“
Quelle: http://de.wikipedia.org/wiki/Computer_Aided_Design |
| CAGD | Computer Aided Geometric Design |
| CAM | Computer Aided Manufacturing (CAM) steht für rechnerunterstützte Fertigung. CAM bezieht sich dabei auf die direkte Steuerung von Produktionsanlagen sowie der unterstützenden Transport– und Lagersysteme. CAM ist ein wesentlicher Bestandteil der computerintegrierten Produktion (Computer Integrated Manufacturing, CIM).
Quelle: http://de.wikipedia.org/wiki/Computer_Aided_Manufacturing |
| Computergrafik | „Die Computergrafik ist ein Teilbereich der Informatik, der sich mit der künstlichen Erzeugung von Bildern mit Hilfe von Computern beschäftigt. Mit derartigen Verfahren erzeugte Bilder nennt man auch Computergrafiken. Verwandte, aber abgegrenzte Fachrichtungen sind Bildverarbeitung, Computer Vision und Mensch-Maschine-Kommunikation. Erstere beiden bilden zusammen mit der Computergrafik und der Informationsvisualisierung die Kernelemente der Computervisualistik.“
Quelle: http://de.wikipedia.org/wiki/Computergraphik |
| Computer-Animation | „Computer-Animation ist eine computerbasierte kontinuierliche Berechnung von Zuständen eines dynamischen Systems zur Darstellung sich in Raum und Zeit verändernder Strukturen durch eine Sequenz aufeinander folgender Bilder.“
Quelle: Maic Masuch, Von Bildern zur Animation, Shaker Verlag 2001 |
| GIS | Ein Geografisches oder (allgemeiner) Geo-Informationssystem (Kurzform GIS) ist ein „rechnergestütztes Informationssystem, das aus Hardware, Software, Daten und den Anwendungen besteht. Mit ihm können raumbezogene Daten digital erfasst und redigiert, gespeichert und reorganisiert, modelliert und analysiert sowie alphanumerisch und grafisch präsentiert werden.“
Quelle: Ralf Bill: Grundlagen der Geoinformationssysteme. Heidelberg 1994 Zit nach: http://de.wikipedia.org/wiki/Geoinformationssystem |
| Freiformkurve | Eine Freiformkurve ist eine Kurve, die sich analytisch nicht exakt beschreiben läßt. Die Kurve sollte möglichst glatt durch viele vorgegebene Punkte laufen.
Quelle: CAD Lexikon: http://www.blien.de/ralf/cad/db/freifrmk.htm |
| Glyphe | In der Typografie ist eine Glyphe die grafische Darstellung eines Schriftzeichens, zum Beispiel eines Buchstabens, eines Silbenzeichens, einer Ligatur oder eines Buchstabenteils. Die Glyphe bildet dabei in sich eine grafische Einheit.
Quelle: http://de.wikipedia.org/wiki/Glyph |
| Rasterizer | Software, mit der Fontdaten für eine konkrete Darstellung als Rastergrafik berechnet werden. Dieser Schritt ist nötig, bevor Fonts am Bildschirm angezeigt oder ausgedruckt werden können.
Quelle: http://www.commando.de/glossar/gloss-r.htm |
| Visualisierung | Visualisierung (im Sinne der Informatik) ist die zielgerichtete Transformation von Daten in ein sichtbares Bild zur Unterstützung der Exploration (Erkundung), Kognition (Erkennen) und Explanation (Erklärung) von Strukturen und Prozessen.
Quelle: http://ifgivor.unimuenster.de/vorlesungen/3D_geovisualisierung/ NeueMedien1_08.htm |
| Bild 1 Pierre Bézier |
 |
| Quelle: http://www.at-mix.de/bezier.htm |
| Bild 2 Kurvenlineal mit Schrauben fixiert
|
 |
| Quelle: http://lo-net.de/home/manfred.distler/Splinevorstellung.ppt#16 |
| Bild 3 Lara Croft, Cyberheldin der Computerspiel-Serie Tomb Raider
|
 |
| Quelle: http://de.wikipedia.org/wiki/Lara_Croft |
| Bild 4 Béziersplines an Übergängen wie z.B. bei 3D-Studio Max
|
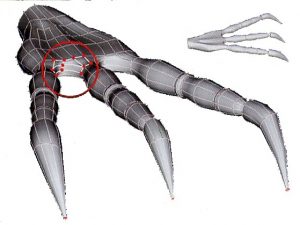 |
| Quelle: Semesteraufgabe im Fach Multimedia- & Webtechnologien, Roman Hagen, 2005 http://goessner.net/download/learn/mwt/ws2005/presentations/BezierSplines.ppt#30 |
[1] Eine Definition des Terms Computergraphik siehe Glossar.
[2] Quelle der Formel als Bitmaps: http://de.wikipedia.org/wiki/Bernsteinpolynom, 26.11.11.
[3] [STRASS96], Eine umfassende Darstellung siehe S. 134 – 138.
[4] [STRASS96], S. 139 – 156.
[5] Vgl.: Christophe Rabut, Departement de Genie Mathematique, Institut National des Sciences Appliquees, 135, avenue de Rangueil, F-31077 TOULOUSE Cedex 4 (France), Quelle: http://www-gmm.insa-toulouse.fr/~rabut/bezier/cad/cad.html 26.11.11.
[6] Paul Cox, The Mathematics of String Art: A Tribute to Pierre Bezier (1910-1999) Quelle: http://members.cox.net/mathmistakes/bezier.htm, 26.11.11.
[7] Vgl.: Dokumentation des Animationsprogrammes Blender in: http://de.wikibooks.org/wiki/Blender_Dokumentation, 26.11.11.
[8] Siehe Bildanhang.
[9] Vgl.: Hauptseminar-Präsentation SS2005, Dr. Ing. Raimund Dachselt: Multimediatechnik, Seite 22, Quelle: http://w3serv.inf.tu-dresden.de/Lehre/Sommersemester_05/Hauptseminar/index.htm, 26.11.11.
[10] Vgl.: http://www.csl.sony.co.jp/person/rekimoto/holowall/, 26.11.11.
[11] Quelle: http://e-collection.ethbib.ethz.ch/ecol-pool/diss/abstracts/p14531.pdf, 12.09.11.
[12] Vgl.: CAD-CAM Report Heft 6/2002, Ein Rückblick auf die CAD/CAM Geschichte, Dressler-Verlag, S. 46.
[13] Vgl.: Dr. T. Meinicke, SVG – Skalierbare Vektorgraphiken – Ein Überblick, Merseburg, 2005, Quelle: http://www.iks.hs-merseburg.de/~meinike/PDF/tekom2004_Wiesbaden_Meinike.pdf, 26.11.11.
[14] Vgl.: http://www.typografie.info/typowiki/index.php, 26.11.11.
[15] siehe Verlesungsfolien „Zeichen und Schriften“, Prof. Husmann, LMU-München; Quelle: http://www-alt.medien.ifi.lmu.de/fileadmin/mimuc/dm_ws04/dm3a.pdf, 26.11.11, Seite 24.
Weitere verwendete Literatur:
[BUNG02] H.-J.Bungartz, M. Griebel, C. Zenger, Einführung in die Computergrafik, 2. Auflage, Vieweg Verlag, Braunschweig, 2002
[STRASS96] J. Encarnacao, W. Straßer, R. Klein, Graphische Datenverarbeitung 1, Oldenbourg 1996
[GORN84] P. Gorny, Interaktive grafische Datenverarbeitung, 1. Aufl., Teubner-Verlag, Stuttgart, 1984
[GRIEG92] I. Grieger, Graphische Datenverarbeitung, 2. Auflage, Springer-Verlag, Berlin, 1992
[MACH00] R. Mach, 3D Visualisierung; 1. Auflage; Galileo Press; Bonn; 2000
[NISCH04] A. Nischwitz, P. Haberäcker, Masterkurs Computergrafik und Bildverarbeitung, Vieweg Verlag, Braunschweig 2004
[RECH02] P. Rechenberg, G. Pomberger, Informatik-Handbuch, 3. Aufl., Hanser-Verlag, München/Wien, 2002
[FOLEY95] J. Foley u. Andere, Computer Graphics: Principles and Practice, 2. Auflage, Addison-Wesley 1995
Fachzeitschriften:
CAD/CAM Report, Dressler-Verlag
Weitere wichtige Links:
Zur Geschichte der Computergraphik: https://design.osu.edu/carlson/history/lessons.html, 26.11.11
Fachbeitrag zu Computerschriften: http://www.mediaforum.ch/fachlexikon, 26.11.11.
Kunstuniversität Linz: Digital Media For Artists: http://www.dma.ufg.ac.at/app, 26.11.11.